Método Simplex

El método simplex es un algoritmo de resolución para modelos de Programación Lineal desarrollado por George Dantzig en el año 1947. Como todo algoritmo cuenta con un proceso iterativo que secuencialmente a través de pasos o iteraciones va aproximando el valor óptimo del problema lineal en caso de existir este último.

Para aplicar el Método Simplex a un modelo de Programación Lineal se requiere que éste último se encuentre en una forma estándar. Para verificar las condiciones del formato estándar se recomienda visitar el siguiente enlace: Programación Lineal - Método Simplex.

El Método Simplex es un método analítico de solución de problemas de programación lineal capaz de resolver modelos más complejos que los resueltos mediante el método gráfico sin restricción en el número de variables.

El Método Simplex es un método iterativo que permite ir mejorando la solución en cada paso. La razón matemática de esta mejora radica en que el método consiste en caminar del vértice de un poliedro a un vértice vecino de manera que aumente o disminuya (según el contexto de la función objetivo, sea maximizar o minimizar), dado que el número de vértices que presenta un poliedro solución es finito siempre se hallará solución.

Ejemplo del Método Simplex

• x1: Número de cinturones tipo A a fabricar por semana.

• x2: Número de cinturones tipo B a fabricar por semana.

A un grupo de artesanos se le presenta la oportunidad exportar cinturones de piel de salmón al mercado europeo. Clasifican los cinturones en dos tipos A y B: A por alta calidad y B por baja calidad. De acuerdo a sus estimaciones tendrían una utilidad de 4 euros por cinturón tipo A y 3 euros por el tipo B. La confección de un cinturón tipo A les requiere el doble de tiempo que uno tipo B. Si confeccionaran sólo cinturones tipo B podrían hacer 1.000 diarios. En todo caso, el abastecimiento de piel es suficiente para confeccionar un total combinado de 800 cinturones diarios. Los cinturones usan un diferente tipo de hebilla según su calidad. Se pueden abastecer de 800 hebillas elegantes al día para los cinturones tipo A y 700 hebillas corrientes al día para los cinturones tipo B. Se desea formular y resolver un modelo de Programación Lineal que permita a los artesanos decidir cuántos cinturones de cada tipo fabricar de modo de maximizar sus ganancias.

1.-Variables de Decisión

2.- Función Objetivo

Cada cinturón tipo A reporta una utilidad de 4 euros y cada cinturón tipo B reporta una utilidad de 3 euros. Se desea maximizar la utilidad total dada por: Max 4x1+3x2

3.-Restricciones

• No se puede fabricar más cinturones tipo A que la cantidad de hebillas disponibles: x1≤800
• No se puede fabricar más cinturones tipo B que la cantidad de hebillas disponibles: x2≤ 700
• Como máximo se puede confeccionar diariamente 800 cinturones del tipo A y del tipo B en conjunto: x1+x2≤800
• La capacidad de producción  permite fabricar 1.000 cinturones tipo B a la semana si se fabricara sólo cinturones de este tipo. Los cinturones tipo A ocupan el doble de recursos que uno B, esto es se pueden fabricar 500 cinturones a la semana si sólo se fabrican cinturones tipo A: 2x1+x2≤1.000
• No negatividad de las variables de decisión: x1, x2 ≥ 0

En términos compactos el modelo de Programación Lineal queda definido por:

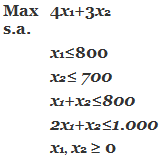
Previo a la aplicación del Método Simplex será necesario llevar el modelo a su forma estándar. Para ello llevamos la función objetivo a minimización y agregamos las variables de holgura no negativas x3, x4, x5,  y x6, para las restricciones 1, 2, 3 y 4, respectivamente.

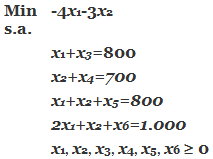
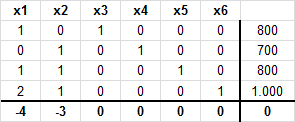
Con ello construimos la tabla inicial del Método Simplex donde las variables de holgura previamente identificadas definen una solución básica factible inicial (no óptima):

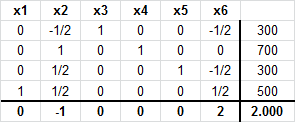
Por el criterio del costo reducido más negativo la variable que ingresa a la base es x1. Luego calculamos en dicha columna el mínimo cuociente que esta dado por: .

En consecuencia el pivote se encuentra en la fila 4 y por tanto la variable x6deja la base. (Notar que para el cálculo del mínimo cuociente o criterio de factibilidad sólo se consideran denominadores que sean estrictamente mayores a cero).

Ahora la variable no básica que ingresa a la base es x2. Calculamos nuevamente el mínimo cuociente sobre dicha columna obteniendo: .

Por tanto x5 abandona la base. Con ello realizamos una nueva iteración del Método Simplex:

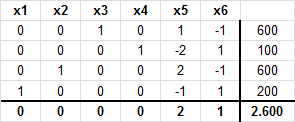
La solución óptima es x1=200 y x2=600, donde el valor de las holguras x3 y x4 corresponde a 600 y 100, respectivamente. Notar adicionalmente que las variables x5 y x6 son no básicas en el óptimo, por tanto su valor es cero, lo que indica que las restricciones 3 y 4 son activas. El valor óptimo del problema es V(P)=2.600.

Para complementar el análisis anterior, se puede apreciar la convergencia del Método Simplex a través de una representación gráfica, realizada en este caso con el software Geogebra. La tabla inicial del Método Simplex corresponde al vértice A (solución básica factible no óptima) del gráfico a continuación, luego al ingresar en primera instancia la variable x1 al cabo de una iteración se alcanza el vértice E (solución básica factible no óptima). Finalmente en la segunda iteración se pasa del vértice E al vértice D, el cual corresponde a la solución básica factible óptima, dado que el costo reducido de las variables no básicas es mayor o igual a cero.

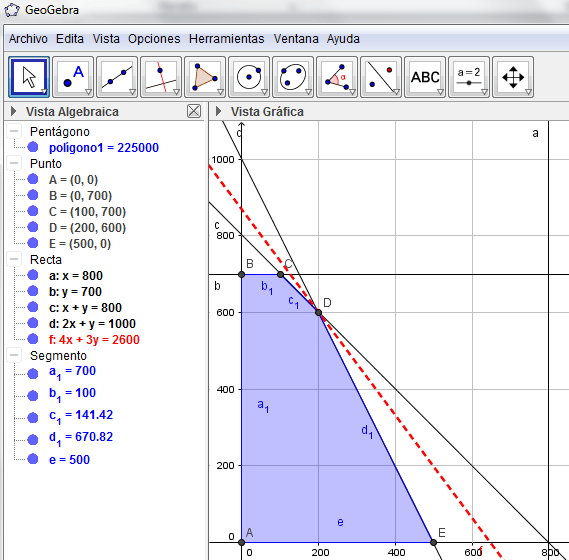
Importante: Una forma de corroborar que el criterio de seleccionar la variable no básica que ingresa a la base como aquella con el costo reducido más negativo se basa en la rapidez de convergencia del Método Simplex y no afecta en su efectividad, consiste en ingresar inicialmente a la base la variable x2. En este caso se puede constatar que se puede alcanzar la solución óptima del problema con un número mayor de iteraciones en comparación al procedimiento detallado en este artículo.