Formulación De Modelos
Una vez definido el problema del tomador de decisiones, la siguiente etapa consiste en reformularlo de manera conveniente para su análisis. La forma convencional en que la investigación de operaciones realiza esto es construyendo un modelo matemático que represente la esencia del problema. El modelo matemático puede expresarse entonces como el problema de elegir los valores de las variables de decisión de manera que se maximice la función objetivo, sujeta a las restricciones dadas. Un modelo de este tipo, y algunas variaciones menores sobre él, tipifican los modelos analizados en investigación de operaciones.
Un paso crucial en la formulación de un modelo de Investigación de Operaciones es la construcción de la función objetivo. Esto requiere desarrollar una medida cuantitativa de la efectividad relativa a cada objetivo del tomador de decisiones identificado cuando se estaba definiendo el problema. Si en el estudio se contemplan mas de un objetivo, es necesario transformar y combinar las medidas respectivas en una medida compuesta de efectividad llamada medida global de efectividad. A veces esta medida compuesta puede ser algo tangible (por ejemplo, ganancias) y corresponder a una meta mas alta de la organización, o puede ser abstracta (como “utilidad”). En este último caso la tarea para desarrollar esta medida puede ser compleja y requerir una comparación cuidadosa de los objetivos y su importancia relativa.
Aplicación: La Oficina responsable del control del agua y los servicios públicos del Gobierno de Holanda, el Rijkswaterstatt, concesionó un importante estudio de Investigación de Operaciones para guiarlo en el desarrollo de una importante política de administración del agua. La nueva política ahorro cientos de millones de dólares en gastos de inversión y redujo el daño agrícola en alrededor de 15 millones de dólares anuales, al mismo tiempo que disminuyo la contaminación térmica y debida a las algas. En lugar de formular un modelo matemático, este estudio de Investigación de Operaciones desarrolló un sistema integrado y comprensible de ¡50 modelos! Mas aún, para alguno de los modelos, se desarrollan versiones sencillas y complejas. La versión sencilla se usó para adquirir una visión básica incluyendo el análisis de trueques. La versión compleja se usó después en las corridas finales del análisis o cuando se deseaba mayor exactitud o más detalles en los resultados. El estudio completo de Investigación de Operaciones involucró directamente a mas de 125 personas – año de esfuerzo (mas de un tercio de ellas en la recolección de datos), creó varias docenas de programas de computación y estructuró una enorme cantidad de datos.
Formulación del Modelo
En la formulación del modelo, podemos ayudarnos con la representación del Problema mediante un organizador gráfico o esquema:
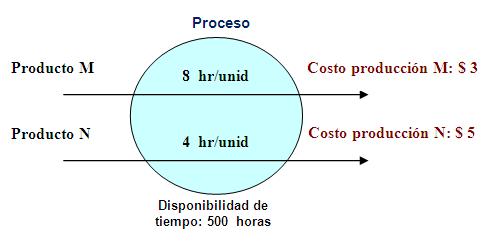
- Definición de Variables
Se desea formular un modelo matemático para determinar la cantidad que debe producirse por cada producto (M y N), por lo tanto tendremos dos variables, representados por: x1 , x2.
Siendo: x1 = Cantidad a producirse del producto M,
x2 = Cantidad a producirse del producto N
- Función Objetivo
Como se tiene información de Costos de producción de los productos M y N, el objetivo será minimizarlos:

Luego la Función Objetivo será Minimizar "C" igual al Costo total de producción del producto M más el Costo total de producción del producto N.
Matemáticamente la Función Objetivo es:

- Definición de Restricciones
El tipo de recurso en el problema es el tiempo (puede ser horas hombre u horas máquina). Formulamos la restricción, colocando en el lado izquierdo de la inecuación el consumo unitario de los productos M y N, y en el lado derecho la cantidad disponible del recurso (500 horas).

Resumiendo tenemos el siguiente Modelo matemático de Programación Lineal del Problema (un modelo con dos variables y una restricción, estando listo para aplicar un método de solución:

2). Líneas de Producción.- Un empresario tiene 80 kg de acero y 120 kg de aluminio, y quiere fabricar dos modelos de bicicletas: bicicletas de paseo y bicicletas de montaña, para venderlas en el mercado a S/. 200 y S/. 150 respectivamente cada modelo, a fin de obtener el máximo beneficio. Para la bicicleta de paseo empleará 1 kg de acero y 3 kg de aluminio, y para la bicicleta de montaña usará 2 kg de ambos metales. Formular el modelo matemático de programación lineal, que permita determinar la cantidad óptima de bicicletas a producir, para obtener el mayor beneficio económico.
Formulación del Modelo
Representamos el Problema mediante un organizador gráfico o esquema

- Definición de Variables:
Se desea determinar la cantidad de bicicletas a producir por cada modelo (paseo y montaña), por lo tanto tendremos dos variables.
Sean: x1 = Cantidad de bicicletas de paseo a fabricar
x2 = Cantidad de bicicletas de montaña a fabricar
- Función Objetivo
El objetivo del problema es maximizar los beneficios económicos totales (Z) de los modelos de bicicletas que fabricará el empresario.
Precio de venta de la bicicleta de paseo = S/. 200
Precio de venta de la bicicleta de montaña = S/. 150
Beneficio económico = Precio de venta unitario x cantidad a fabricar
Beneficio económico total de bicicleta de paseo = 200 x1
Beneficio económico total de bicicleta de montaña = 150 x2
Luego la Función objetivo será: Maximizar: Z = 200 x1 + 150 x2
- Definición de Restricciones
Elaboramos una tabla de materia prima consumida (Acero y Aluminio) por cada modelo de bicicleta (paseo y montaña) y su disponibilidad:
Modelo de bicicleta
|
Acero
|
Aluminio
| |
Paseo
|
1 kg.
|
3 kg.
| |
Montaña
|
2 kg.
|
2 kg.
| |
Disponibilidad de materia prima
|
80 kg.
|
120 kg.
| |
Restricción del consumo de Acero en la fabricación de bicicletas:
1 x1 + 2 x2 < 80
Restricción del consumo de Aluminio en la fabricación de bicicletas:
3 x1 + 2 x2 < 120
Observación:
- El lado derecho de las restricciones, 80 y 120 representa la disponibilidad en kg. de acero y aluminio respectivamente (materia prima).
- El lado izquierdo en las restricciones indica el consumo unitario de materia prima por cada modelo de bicicleta.
- Condición de no negatividad: La producción de cada modelo de las bicicletas pueden ser cero (0) o mayor que cero, o sea: x1, x2 = 0
Luego el Modelo matemático de Programación Lineal (con dos variables y dos restricciones) será:
No hay comentarios.:
Publicar un comentario